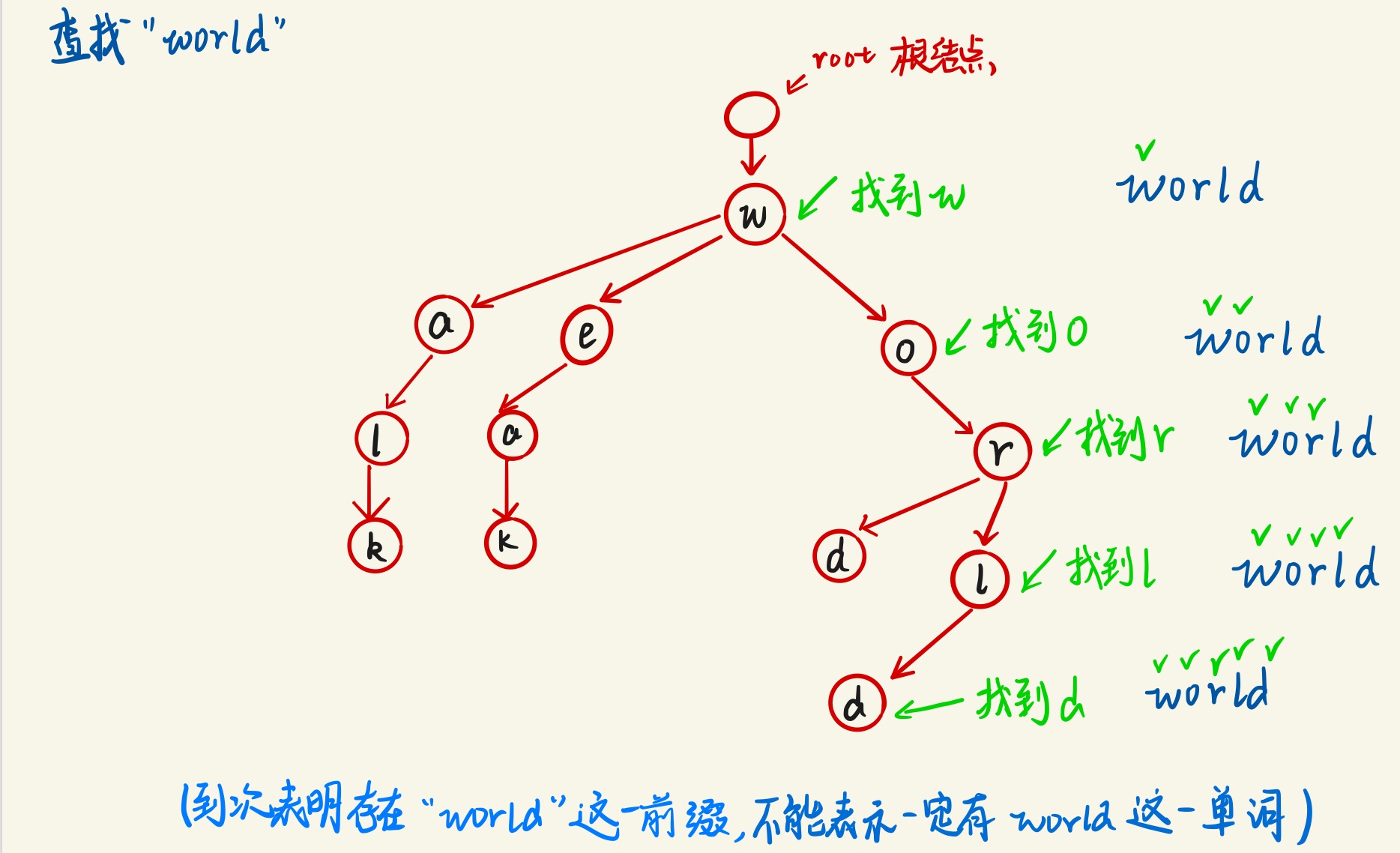
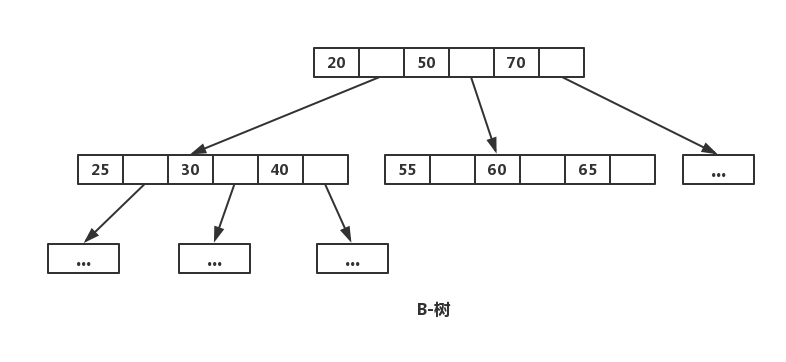
树的三种存储结构

树：树和森林 森林和二叉树的转换 树和森林的遍历 二叉排序树和平衡排序树在总结查找的时候再说

建立树和二叉树的关系，将树的操作转换成二叉树的简单操作

树和森林的表示方法 树的三种存储结构 双亲表示法

实际上就是一个数组形式。数组中的每个元素存放两部分信息，一个是自身的值，一个是双亲的下标。

c语言类型描述

#define MAX_TREE_SIZE 100
typedef struct PTNode{Elem data;int parent;//双亲位置域
}PTNode;//树结构
typedef struct{PTNode nodes[MAX_TREE_SIZE];int r,n;//根结点位置和结点个数
}PTree;

孩子链表表示法

用一个数组来存放二叉链表的结点，数组元素包含结点自身的值和一个链表的头，这个链表由它所有的孩子串在一起构成。

下图是一个双亲-孩子链表表示法，把双亲那一列去掉就是孩子链表表示法。

孩子表示法定义：把每个结点的孩子排列起来，以单链表作存储结构，则n个结点有n个孩子链表，如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中。

C语言类型描述

//孩子结点结构
typedef struct CTNode{int child;struct CTNode* nextchild;
}*ChildPtr;//双亲结点结构
typedef struct {Elem data;ChildPtr firstchild;//孩子链表的头指针
}CTBox;//树结构
typedef struct{CTBox nodes[MAX_TREE_SIZE];int r,n;//根结点位置和结点数
}CTree;

树的二叉链表（孩子-兄弟）存储表示法

每个结点有两个指针域，左指针域指向第一个孩子，右指针域指向它的右邻兄弟

同时孩子-兄弟表示法本身可以看成一棵二叉树

两棵二叉树为唯一的对应关系

把原来的二叉树的根去掉，变成一个森林。把孩子-兄第表示法的根也去掉，发现二者仍然对应。

c语言的类型描述

typedef struct CSNode{Elem data;struct CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;

森林和二叉树的转换 森林和二叉树的对应关系

设 森 林 : F = ( T 1 , T 2 , 。 。 。 , T n ) ; 森 林 含 有 n 棵 树 T 1 = ( r o o t , t 11 , t 12 , 。 。 。 , t 1 m ) ; 第 一 棵 树 T 1 ， 树 根 为 r o o t ， 子 树 为 t 11 , t 12 , 。 。 。 , t 1 m 二 叉 树 : B = ( L B T , N o d e ( r o o t ) , R B T ) ; 根 r o o t ， 左 子 树 L B T ， 右 子 树 R B T 由 森 林 转 换 成 二 叉 树 的 转 换 规 则 为 ： 若 F = ∅ , 则 B = ∅ 否 则 ， 由 R O O T ( T 1 ) 对 应 得 到 N o d e ( r o o t ) ; 由 ( t 11 , t 12 , 。 。 。 , t 1 m ) 对 应 得 到 L B T ; 由 ( T 2 , T 3 , 。 。 。 , T n ) 对 应 得 到 R B T 由 二 叉 树 转 换 为 森 林 的 转 换 规 则 为 ： 若 B = ∅ , 则 F = ∅ 否 则 ， 由 N o d e ( r o o t ) 对 应 得 到 R O O T ( T 1 ) ; 由 L B T 对 应 得 到 ( t 11 , t 12 , 。

。 。 , t 1 m ) ; 由 R B T 对 应 得 到 ( T 2 , T 3 , 。 。 。 , T n ) ; \begin{array}{ll} 设森林: &\\ F=(T_1,T_2,。。。,T_n); & 森林含有n棵树\\ T_1=(root,t_{11},t_{12},。。。,t_{1m}); &第一棵树T_1，树根为root，子树为t_{11},t_{12},。。。,t_{1m}\\ \\ 二叉树: \\ B=(LBT,Node(root),RBT); & 根root，左子树LBT，右子树RBT\\ \\ \\ 由森林转换成二叉树的转换规则为：\\ 若F=\ ,则B=\ \\ 否则，\\ 由ROOT(T_1)对应得到Node(root);\\ 由(t_{11},t_{12},。。。,t{1m})对应得到LBT;\\ 由(T_2,T_3,。。。,T_n)对应得到RBT\\ \\ 由二叉树转换为森林的转换规则为：\\ 若B=\ ,则F=\ \\ 否则，\\ 由Node(root)对应得到ROOT(T_1);\\ 由LBT对应得到(t_{11},t_{12},。

。。,t_{1m});\\ 由RBT对应得到(T_{2},T_{3},。。。,T_{n});\\ \end{array} 设森林:F=(T1​,T2​,。。。,Tn​);T1​=(root,t11​,t12​,。。。,t1m​);二叉树:B=(LBT,Node(root),RBT);由森林转换成二叉树的转换规则为：若F=∅,则B=∅否则，由ROOT(T1​)对应得到Node(root);由(t11​,t12​,。。。,t1m)对应得到LBT;由(T2​,T3​,。。。,Tn​)对应得到RBT由二叉树转换为森林的转换规则为：若B=∅,则F=∅否则，由Node(root)对应得到ROOT(T1​);由LBT对应得到(t11​,t12​,。。。,t1m​);由RBT对应得到(T2​,T3​,。。。,Tn​);​森林含有n棵树第一棵树T1​，树根为root，子树为t11​,t12​,。。。,t1m​根root，左子树LBT，右子树RBT

树转换为二叉树

将一棵树转换为二叉树的思路，主要是根据树的孩子-兄弟存储方式而来的，方法是：

（1）树中所有相邻兄弟之间加一条连线

（2）对树中的每个结点，只保留其与第一个孩子结点之间的连线，删去其与其它孩子结点之间的连线。

（3）以树的根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明。

可以证明，树做这样的转换所构成的二叉树是唯一的。

这样转换出来的二叉树是无右子树的！

森林转换为二叉树

森林是若干棵树的集合。树可以转换为二叉树，森林同样也可以转换为二叉树。因此，森林也可以方便地用于孩子-兄弟结点表示。森林转换为二叉树的方法如下：

（1）将森林中的每棵树转换成相应的二叉树。

（2）第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子，当所有二叉树连在一起后，所得到的二叉树就是森林转换得到的二叉树。

上面看出每个二叉树都是无右子树的，所以可以将很多二叉树连成一个。

二叉树还原为树或森林

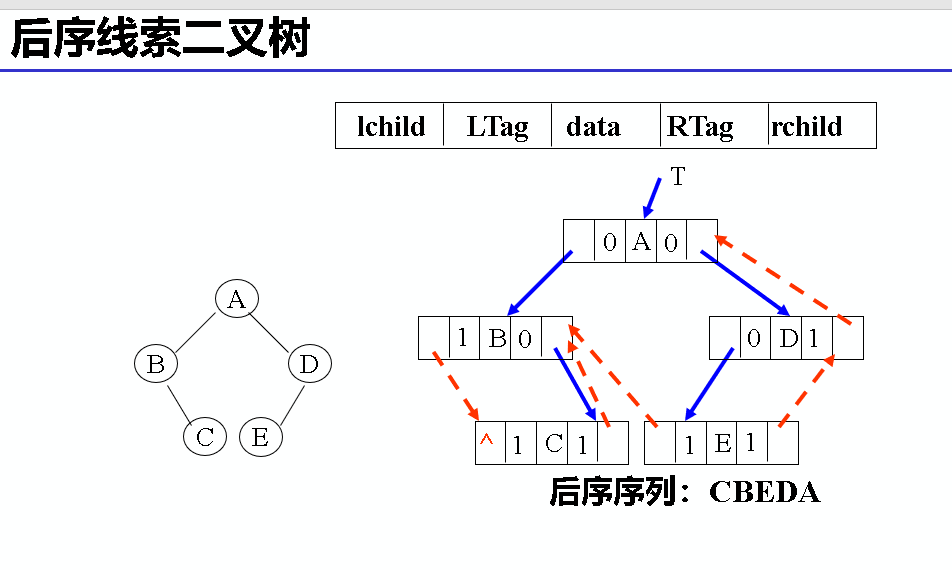
树和森林都可以转换为二叉树，二者的不同是：树转换成的二叉树，其根结点必然无右孩子，而森林转换后的二叉树，其根结点有右孩子。将一棵二叉树还原为树或森林，具体方法如下：

（1）若某结点是其双亲的左孩子，则把该结点的右孩子、右孩子的右孩子…都与该结点的双亲结点用线连起来。

（2）删掉原二叉树中所有双亲结点与右孩子结点的连线。

（3）整理由（1）、（2）两步所得到的树或森林，使之结构层次分明。

归纳总结：

n个结点的树有多少种形态？

解析：可通过树的二叉树表示来估计。在树的二叉树表示中，根的右指针一定是空的，因此，估计有多少种形态看根的左子树的n-1个结点能构成多少种二叉树。根据在二叉树中的分析可知，它服从函数。

树和森林的遍历

树的遍历可以有一下搜索路径：

1.先根（次序）遍历：

若树不空，则先访问根结点，然后依次先根遍历各棵子树。

2.后根（次序）遍历：

若树不空，则依次后根遍历各棵子树，然后访问根结点。

3.按层次遍历：

若树不空，则自上而下自左向右访问树中每个结点。

先根遍历时顶点的访问次序：

A B E F C D G H I J K

后根遍历时顶点的访问次序：

E F B C I J K H G D A

层次遍历时顶点的访问次序：

A B C D E F G H I J K

森林可以分解成三部分：

（1）森林中第一棵树的根结点

（2）森林中第一棵树的子树森林

（3）森林中其它树构成的森林

先序遍历：若森林不空，则访问森林中第一棵树的根结点；先序遍历森林中第一棵树的子树森林；先序遍历森林中（除第一棵树之外）其余树构成的森林。

即：依次从左至右对森林中的每一棵树进行先根遍历。

中序遍历：

若森林不空，则中序遍历森林中第一棵树的子树森林；访问森林中第一棵树的根结点；中序遍历森林中（除第一棵树之外）其余树构成的森林。

即：依次从左至右对森林中的每一棵树进行后根遍历。

树的遍历和二叉树遍历的对应关系？

树的遍历的应用

例：求森林的深度？

设树的存储结构为孩子-兄弟链表

typedef struct CSNode{ElemType data;struct CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;int Depth(CSTree T)
{if(T==NULL) return 0;else{d1=Depth(T->firstchild);d2=Depth(T->nextsibling);return Max{d1+1,d2};}
}

哈夫曼树和哈夫曼编码 最优树的定义

在所有含n个叶子结点、并带相同权值的m叉树中，必存在一棵其带权路径长度取最小值的树，称为最优树。

哈夫曼树：给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树( Tree)。

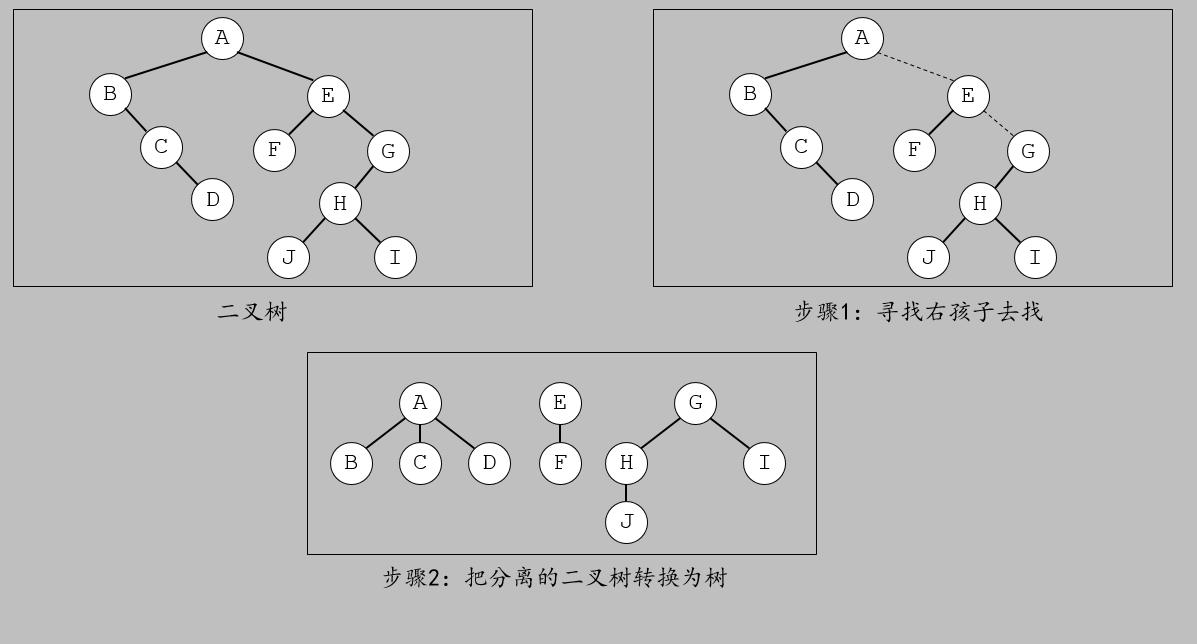
树的特征：

权值小的节点离根节点远，权值大的节点离根节点近。

如何构造最优树

哈夫曼算法：

根据给定的n个权值{w1,w2,…,wn},构造n棵二叉树的集合F={T1,T2,…,Tn}其中每棵二叉树中均只含一个带权值为w1的根结点，其左、右子树为空树；在F中选取其根结点的权值为最小的两棵二叉树，分别作为左、右子树构造一棵新的二叉树，并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和；从F中删去这两棵树，同时加入刚生成的新树；重复2和3，直到F中只含一棵树为止。 哈夫曼编码

哈夫曼编码思想：将构成电文的每个不同字符作为叶子节点，其权值为电文中字符的使用频率或次数，构造哈夫曼树。此哈夫曼树中从根到每个叶子节点都有一条唯一的路径，对路径上各分支约定，左分支标识为’0’码，右分支标识为‘1’码，则从根结点到叶子结点的路径上分支的‘0’、‘1’码组成的字符串即为该叶子结点的哈夫曼编码。

例子：已知权值W={5，6，2，9，7}

F中有5棵二叉树：{5} {6} {2} {9} {7}

找两个权值最小的：{5},{2}，合并,根结点为5+2=7，5和2谁是左子树无所谓（树不唯一，但是WPL唯一）

F中剩下：{6} {9} {7} {7}

再选 {6} {7} ，选哪个{7}？都行（树不唯一） 合并，根结点为6+7=13

F中剩下：{9} {7} {13}

选{9} {7},根结点 9+7=16

剩下：{13} {16} 合并

令左分支为0，右分支为1，从上到下，进行编码：

定长编码：正反译码都不会出现歧义，不能保证电文总长最短

变长编码：使用频率高的短一点，频率低的长一点，能降低电文总长度；但是反着没法译码

出现歧义的根源是因为对于变长编码，存在两个编码a、b，其中a是b的子字符串。

为了消除歧义，提出了前缀编码。

前缀编码：若要设计长短不等的编码，则必须是任意一个字符的编码都不是另外一个字符编码的前缀，这种编码称作前缀编码。

编码：

树是二叉最优树，频率越高编码越短，符合电文总长最短。都是根结点到叶子节点的编码，叶子节点不是根结点的双亲，所以不是任何编码的子字符串。

所以编码是前缀编码。

例子：数据传送中的二进制编码，要传送数据state，seat，act，tea，cat，set，a，eat，如何使传送的长度最短？

首先，规定二叉树的构造为左走0，右走1.

为了保证长度最短，先看字符出现的次数，然后将出现次数当作权，如下图所示。

字符staec

字符出现次数

{3} {8} {7} {5} {2}

{8} {7} {5} {5:3,2}

{8} {7} {10:5,5:3,2}

{15:8,7} {10:5,5:3,2}

{25:15:8,7,10:5,5:3,2}

二叉排序树和平衡排序树在总结查找的时候再说