33 流模型

1

一小节中讲到了 Model（LVM），VAE。其主要思想就是将隐变量扩充 在上 高维连续的分布，来增强模型的表达能力。而 LVM 模型中的核心困难是 P(X) 计算不出来，因为 P ( X ) = ∫ Z P ( X ∣ Z ) P ( Z ) d Z , P(X)=\int_{Z} P(X \mid Z) P(Z) d Z, P(X)=∫Z​P(X∣Z)P(Z)dZ, 而 Z Z Z 的维度过高 P ( X ) P(X) P(X) 算不出来。而根据 公式：

P ( Z ∣ X ) = P ( Z ) P ( X ∣ Z ) P ( X ) P(Z \mid X)=\frac{P(Z) P(X \mid Z)}{P(X)} P(Z∣X)=P(X)P(Z)P(X∣Z)​

所以导致 P ( Z ∣ X ) P(Z \mid X) P(Z∣X) 无法计算。而 VAE ⁡ \{VAE} VAE 那章介绍了近似推断的方法, 使用一个简单分布 Q ϕ ( Z ∣ X ) Q_{\phi}(Z \mid X) Qϕ​(Z∣X) 来近

似 P ( Z ∣ X ) , P(Z \mid X), P(Z∣X), 其中还使用重参数化技巧来用一个神经网络来代替分布。 而在 VAE 中通过优化变分下界 ELBO 来达到最终优化的目的，而不是直接对 Log 似然函数进行 优化。所以当然会有误差了。那么这将启发我们，可不可以绕过这个 的 P(Z)，使模型变

得 。

2 Flow based Model

什么是flow model 呢？首先用一张图来进行表示：

可以用一个简单的例子来简单的介绍 Flow model。X 可以代表是当前的自己，人是比较复杂的， 所以 X → P X ( X ) X \ P_{X}(X) X→PX​(X) 计算非常困难。而一般昨天的我 Z k → P Z k ( Z k ) , Z_{k} \ P_{Z_{k}}\left(Z_{k}\right), Zk​→PZk​​(Zk​), 比今天要简单一点，但是很有可 能，昨天的我依然很复杂，无法计算。那么，就不但的往前推，到了刚出生的时候 Zo，这时肯定是非常筒单的， Z 0 → P Z 0 ( Z 0 ) Z_{0} \ P_{Z_{0}}\left(Z_{0}\right) Z0​→PZ0​​(Z0​) 婴儿的世界里是非黑即白的，此时的分布很筒单，可以被假设性 N ( 0 , I ) \{N}(0, I) N(0,I) 。而 这个过程：

P Z 0 ( Z 0 ) → P Z 1 ( Z 1 ) → P Z 2 ( Z 2 ) ⋯ → P Z k ( Z k ) → P X ( X ) P_{Z_{0}}\left(Z_{0}\right) \ P_{Z_{1}}\left(Z_{1}\right) \ P_{Z_{2}}\left(Z_{2}\right) \cdots \ P_{Z_{k}}\left(Z_{k}\right) \ P_{X}(X) PZ0​​(Z0​)→PZ1​​(Z1​)→PZ2​​(Z2​)⋯→PZk​​(Zk​)→PX​(X)

就被称为“流”。因为流模型中初始分布是很簡单的。极大似然估计中求的是：arg max P ( X ) P(X) P(X) 。那么下 一个问題就是如何建立 X 和 Z 之间的关系，将 a r g m a x P ( X ) arg max P(X) (X) 转换成求关于 P ( Z o ) P(Z_{o}) P(Zo​) 的函数。

3 of

假设 X = f ( Z ) , Z , X ∈ R p X=f(Z), Z, X \in \{R}^{p} X=f(Z),Z,X∈Rp 。而 Z ∼ P Z ( Z ) , X ∼ P X ( X ) ; f Z \sim P_{Z}(Z), X \sim P_{X}(X) ; f Z∼PZ​(Z),X∼PX​(X);f 是一个光滑可逆的函数。

那么可以得到：

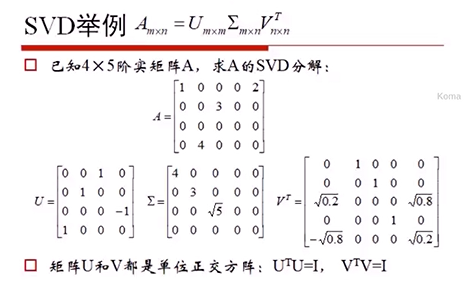
∫ Z P Z ( Z ) d Z = 1 = ∫ X P X ( X ) d X \int_{Z} P_{Z}(Z) d Z=1=\int_{X} P_{X}(X) d X ∫Z​PZ​(Z)dZ=1=∫X​PX​(X)dX

根据不定积分的性质可以得到：

∣ P Z ( Z ) d Z ∣ = ∣ P X ( X ) d X ∣ P X ( X ) = ∣ d Z d X P Z ( Z ) ∣ \begin{array}{c} \left|P_{Z}(Z) d Z\right|=\left|P_{X}(X) d X\right| \\ \\ P_{X}(X)=\left|\frac{d Z}{d X} P_{Z}(Z)\right| \end{array} ∣PZ​(Z)dZ∣=∣PX​(X)dX∣PX​(X)=∣∣​dXdZ​PZ​(Z)∣∣​​

而 X = f ( Z ) X=f(Z) X=f(Z) 且 f f f 是光滑可逆的，所以 Z = f − 1 ( X ) , Z=f^{-1}(X), Z=f−1(X), 那么有

P X ( X ) = ∣ ∂ f − 1 ( X ) ∂ X ∣ P Z ( Z ) P_{X}(X)=\left|\frac{\ f^{-1}(X)}{\ X}\right| P_{Z}(Z) PX​(X)=∣∣∣∣​∂X∂f−1(X)​∣∣∣∣​PZ​(Z)

但是实际上 Z 和 X 都是高维变量，所以 ∂ f − 1 ( X ) ∂ X \frac{\ f^{-1}(X)}{\ X} ∂X∂f−1(X)​ 是一个 。熟悉矩阵的朋友应该知道，矩阵代表了一个变换，而矩阵行列式的值则代表了变换的尺度。而在计算中我们关注的是矩阵变换的尺度，所以，

P X ( X ) = ∣ det ⁡ ( ∂ f − 1 ( X ) ∂ X ) ∣ P Z ( Z ) P_{X}(X)=\left|\{det}\left(\frac{\ f^{-1}(X)}{\ X}\right)\right| P_{Z}(Z) PX​(X)=∣∣∣∣​det(∂X∂f−1(X)​)∣∣∣∣​PZ​(Z)

而最终的目的是想将 P X ( X ) P_{X}(X) PX​(X) 完全用一个 Z Z Z 为自变量的函数来表达，所以要将 ∣ ∂ f − 1 ( X ) ∂ X ∣ \left|\frac{\ f^{-1}(X)}{\ X}\right| ∣∣∣​∂X∂f−1(X)​∣∣∣​ 用 Z Z Z 来表示。 下面先写结论

P X ( X ) = ∣ det ⁡ ( ∂ f − 1 ( X ) ∂ X ) ∣ P Z ( Z ) = ∣ det ⁡ ( ∂ f − 1 ( Z ) ∂ Z ) ∣ − 1 P Z ( Z ) \begin{} P_{X}(X) &=\left|\{det}\left(\frac{\ f^{-1}(X)}{\ X}\right)\right| P_{Z}(Z) \\ &=\left|\{det}\left(\frac{\ f^{-1}(Z)}{\ Z}\right)\right|^{-1} P_{Z}(Z) \end{} PX​(X)​=∣∣∣∣​det(∂X∂f−1(X)​)∣∣∣∣​PZ​(Z)=∣∣∣∣​det(∂Z∂f−1(Z)​)∣∣∣∣​−1PZ​(Z)​

这个结论是怎么来的呢？我们来看一个简单的例子，如下图所

如图所示， y = f ( x ) , x = f − 1 ( y ) y=f(x), x=f^{-1}(y) y=f(x),x=f−1(y) 。那么有

d y d x = ∂ f ( x ) ∂ x , d x d y = ∂ f − 1 ( y ) ∂ y \frac{d y}{d x}=\frac{\ f(x)}{\ x}, \frac{d x}{d y}=\frac{\ f^{-1}(y)}{\ y} dxdy​=∂x∂f(x)​,dydx​=∂y∂f−1(y)​

而，

∂ f ( x ) ∂ x ∂ f − 1 ( y ) ∂ y = 1 \frac{\ f(x)}{\ x} \frac{\ f^{-1}(y)}{\ y}=1 ∂x∂f(x)​∂y∂f−1(y)​=1

在本文举的例子中，

( f − 1 ) ′ ( a ) = b − c a − c ( f ) ′ ( b ) = a − c b − c \begin{} \left(f^{-1}\right)^{\prime}(a) &=\frac{b-c}{a-c} \\ (f)^{\prime}(b) &=\frac{a-c}{b-c} \end{} (f−1)′(a)(f)′(b)​=a−cb−c​=b−ca−c​​

很显然有 ( f − 1 ) ′ ( a ) f ′ ( b ) = 1. \left(f^{-1}\right)^{\prime}(a) f^{\prime}(b)=1 . (f−1)′(a)f′(b)=1. 这就是 of 。我们可以得到两个变量之间关于 映射 f f f 的转换为：

P X ( X ) = ∣ det ⁡ ( ∂ f − 1 ( Z ) ∂ Z ) ∣ − 1 P Z ( Z ) P_{X}(X)=\left|\{det}\left(\frac{\ f^{-1}(Z)}{\ Z}\right)\right|^{-1} P_{Z}(Z) PX​(X)=∣∣∣∣​det(∂Z∂f−1(Z)​)∣∣∣∣​−1PZ​(Z)

那

么，当训练完成之后，从 P(Z) 中采样比较筒单，通过上述公式，就叶以得到 P ( X ) , P(X), P(X), 所以 P ( X ) P(X) P(X) 是可求解的。如何学习呢？其实并不难，通过极大似然估计可以得到：

log ⁡ P X ( X ) = log ⁡ ∣ det ⁡ ( ∂ f − 1 ( Z ) ∂ Z ) ∣ − 1 + log ⁡ P Z ( Z ) \log P_{X}(X)=\log \left|\{det}\left(\frac{\ f^{-1}(Z)}{\ Z}\right)\right|^{-1}+\log P_{Z}(Z) logPX​(X)=log∣∣∣∣​det(∂Z∂f−1(Z)​)∣∣∣∣​−1+logPZ​(Z)

那么：

∂ log ⁡ P X ( X ) ∂ X = ∂ log ⁡ ∣ det ⁡ ( ∂ f − 1 ( Z ) ∂ Z ) ∣ − 1 + log ⁡ P Z ( Z ) ∂ Z ∂ Z ∂ X = ∂ log ⁡ ∣ det ⁡ ( ∂ f − 1 ( Z ) ∂ Z ) ∣ − 1 + log ⁡ P Z ( Z ) ∂ Z ∂ f − 1 ( X ) ∂ X \begin{} \frac{\ \log P_{X}(X)}{\ X} &=\frac{\ \log \left|\{det}\left(\frac{\ f^{-1}(Z)}{\ Z}\right)\right|^{-1}+\log P_{Z}(Z)}{\ Z} \frac{\ Z}{\ X} \\ &=\frac{\ \log \left|\{det}\left(\frac{\ f^{-1}(Z)}{\ Z}\right)\right|^{-1}+\log P_{Z}(Z)}{\ Z} \frac{\ f^{-1}(X)}{\ X} \end{} ∂X∂logPX​(X)​​=∂Z∂log∣∣∣​det(∂Z∂f−1(Z)​)∣∣∣​−1+logPZ​(Z)​∂X∂Z​=∂Z∂log∣∣∣​det(∂Z∂f−1(Z)​)∣∣∣​−1+logPZ​(Z)​∂X∂f−1(X)​​

由于f 的逆很要求，上述梯度的计算还是比较简单的。然而，关于大矩阵行列式的计算并不美丽。后

续有很多针对这点的改进方法，有兴趣的同学自行查看flow based 的论文。

[1] ICLR 2015 NICE-Non-

[2] ICLR 2017 using Real NVP

[3] 2018 Glow: Flow with 1×1

4 小结

本章主要介绍的是流模型的主要思想，在 Model 经常会遇到后验过于复杂无法求解的问题。流模型绕开了这个部分，对更简单的分布建模，然后建立原分布与简单分布之间的映射关系。个人觉得Stein 变分梯度下降就有点流模型的影子在里面。在建立映射关系是用到了重要的 of ，并之后介绍了变化后的目标函数和梯度求解方法。