生活中数列的例子有哪些（常见的数列分析）

在大多数人的潜意识里，数学的发现来自于对自然生命的观察和归纳，从一些具体的事物中总结出一套规律，在数学演绎体系中深入研究，最终得到更多一般结论。有时，我们很幸运能够得到一些应用非常广泛的数学定律。今天，我们来聊一聊数学中最著名的数学现象之一——斐波那契数列。

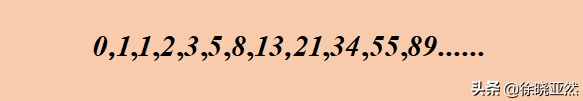
这个序列的名字比较有风格，是一个人的名字。 1202年，意大利数学家斐波那契出版了《算盘全书》，他是第一个系统研究这个数列相关性质的人。

这个序列定义如下：

前两项是0,1；从第3项开始，后一项为前两项之和。

斐波那契，欧洲中世纪伟大的数学家

斐波那契出生于 1175 年。他的父亲在北非做生​​意。这个年轻人从很小的时候就开始协助父亲工作。在协助父亲经商的过程中，他接触到了阿拉伯数字，发现了阿拉伯数字。书籍联想比罗马数字更简洁，更容易记住。在过去几年的听闻过程中，斐波那契不断总结出一些计算技巧。于是他到地中海地区向当地的数学家学习，经过几年的学习和总结。 1200年回国后，他将自己在计算方面的经验和研究写成代表作《珠算全书》。这本书记录了很多利率、记账、会计，在当时是一本非常实用的会计教科书。这本书诞生于中世纪的欧洲，对当时的人们应该算是数学计算的启蒙书籍。

我们从数学上得到这个序列的递归关系：

斐波那契数列递归关系

其实就递推关系而言，计算这个数列的每一项很容易，但是通项公式就不是那么明显了，至少在中学时代的数学知识上，很难解这个序列的通式公式就出来了。在这里，小冉只介绍了一个看起来很“简单”的解决方案——特征值法。

特征值法求解斐波那契数列通项公式

我们不会详细说明为什么要这样使用特征值方法。我们只是用一个简单的方法求解这个数列的通项公式，结果应该更容易让大家接受。

很多人第一次很难接受斐波那契数列的通项公式。为什么这个顺序如此违反直觉？明明都是自然数列，为什么通项公式中有两个无理数的n次方形式？

其实很容易推导出其公式的推导过程。这里的 λ1 和 λ2 不是普通的无理数。这两个数之间有两个特殊的性质，分别是：λ1=λ2-1，1/λ1=λ2。 0.618 和 1.618 也称为黄金比例共轭。正是由于这个性质，在通项公式中，两个无理数的n次方的小数部分总是可以相互抵消，最后只能存在自然数部分。在研究数列时，如果能找到通项公式，那么它的性质就基本揭示了。

小然曾经在中学参加过一次信息学竞赛，其中一道编程题是这样描述的：

有一个十级楼梯，你可以选择一次跳一级，或者两级。一共有多少次跳跃？

当我收到这个问题时，很容易想到复杂的方面。想了想，发现无法按照题意直接写出方法，只好先画图。给几个看看结果。

跳至关卡 1：1 种；

跳到2级：1+1=2种；

跳到3级：1+2=3种；

跳到4级：2+3=5种；

...

这后面的数字不只是斐波那契数列，所以这个编程问题就成功解决了。当然，斐波那契在定义这个数字序列时并没有使用这个例子。他举了养兔子的例子，也很形象。

黄金比例的模型，雅典的帕台农神庙

这个世界上有成千上万的序列。为什么这个序列最有名？恐怕很大程度上是因为黄金比例体现在这个序列上。我们都知道，斐波那契数列的后一项与前一项相比会逐渐接近黄金比例。通式公式推导过程中的Ф是黄金比例，也是大自然美好形象的代名词。自然界中的许多事物都反映了这个美丽的数字。还记得上一篇文章中提到的连续分数形式吗？连分数可以用最简单的方式来描述黄金比例，λ2=1....=[1;1,1,1,1...],

λ1=0....=[0;1,1,1,1...].

在摄影中，通常在取景器中设置一种称为斐波那契螺旋线的方法，而不是普通的三段式图案。这样的螺旋是怎么形成的？

斐波那契螺旋构图在摄影中的应用

以1*1的方格为初始位置，顺时针或逆时针分别构造2*2、3*3、5*5、8*8方格，然后从每个方格的二分之一圆中取出四个方格。由于所有正方形部分都沿同一方向旋转，因此相邻正方形的弧可以首尾相连，从而形成斐波那契螺旋线。

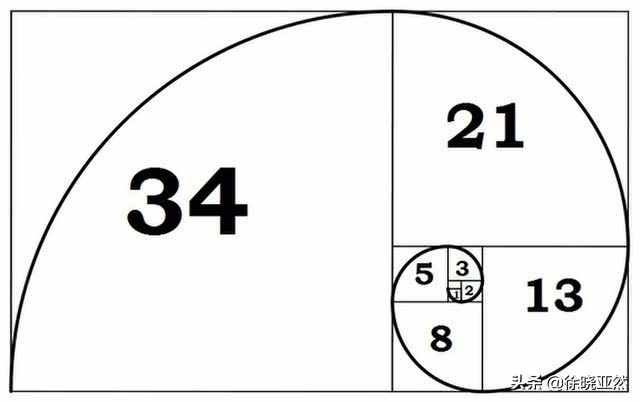
斐波那契螺旋线

这样的构图，重点可以很突出，照片看起来更自然逼真。

我们来做一个很有意思的话题，特意把斐波那契的元素写成下面的形式，积累起来。

斐波那契数列分割分数和

你认为如果把斐波那契数列的每一项都分成这样的小数，然后相加，最终的结果会是什么？还会有另一个莫名其妙的超越数吗？不过，凡事总有例外，但小然想告诉大家，这个和其实是一个很简单的有理数。

拆分小数和的推导过程

您没看错，结果是相当清脆的 1/89！非常感谢您第一个发现这个结果！

相信很多人都看过并想过下图。

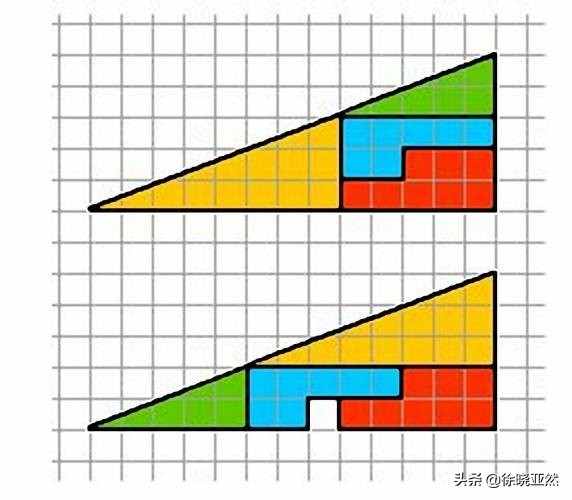
多余的区域1是怎么来的

上下图明明是一样的，为什么下图中有个小方块？

让我们来探讨一下原因。如果我们仔细观察，我们可以发现，这两个“大三角形”所形成的两条斜边线的斜率不同。小绿色三角形的斜率为 2/5，黄色三角形的斜率为 2/5。斜率为3/8，是不同的斜率，说明两条线段实际上并不共线，但由于斜率相差不大，所以在允许绘制误差的情况下看起来像一条线。直截了当。

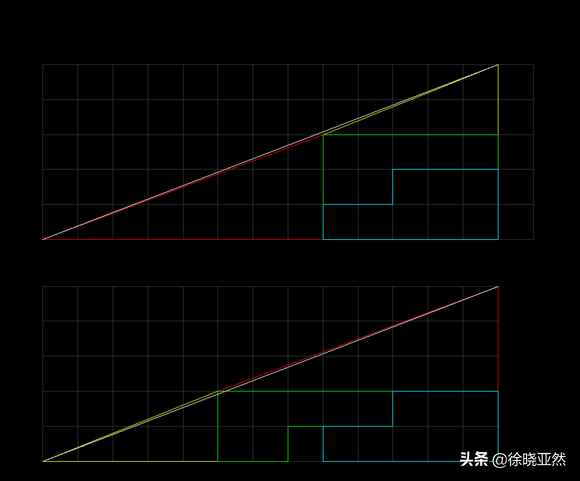
用CAD精确绘制，可以发现斜边上重叠的部分不一样

如果你用精确的绘图工具测量，你会发现斜边上的黄色三角形和绿色三角形的固定点实际上并不会与网格的点重合，而是会稍微向“大三角形” ” 在外面，就是这样一个轻微的错误，在视觉上“偷偷”隐藏了一个1的区域。这个经典的视觉错误技巧是 1953 年由纽约市的业余魔术师 Paul Curry 发明的。

说起来，这个有趣的小技巧和斐波那契数列有什么关系吗？当然，这很重要。图中不同颜色部分的边长按从小到大的顺序排列，1、2、3、5、8、13，不都是序列中的元素吗？重点看斜边斜边的组成，2,5,3,8，满足2×8=3×5-1。由此我们不得不写出斐波那契数列的一个重要关系：

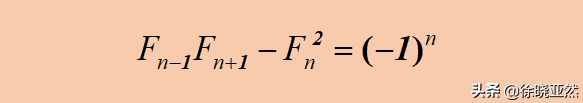
视觉魔法的根源

这个公式是上述图形构造的根源。当然，我们也可以通过其他的阵元，构建出更加微妙、不易察觉的视觉魔法！有兴趣的同学可以自己试试。

斐波那契数列本身就是一系列自然数的组合，所以肯定和数论有关。例如，我们可以很容易地从阳辉三角形中“拉”出斐波那契数列。

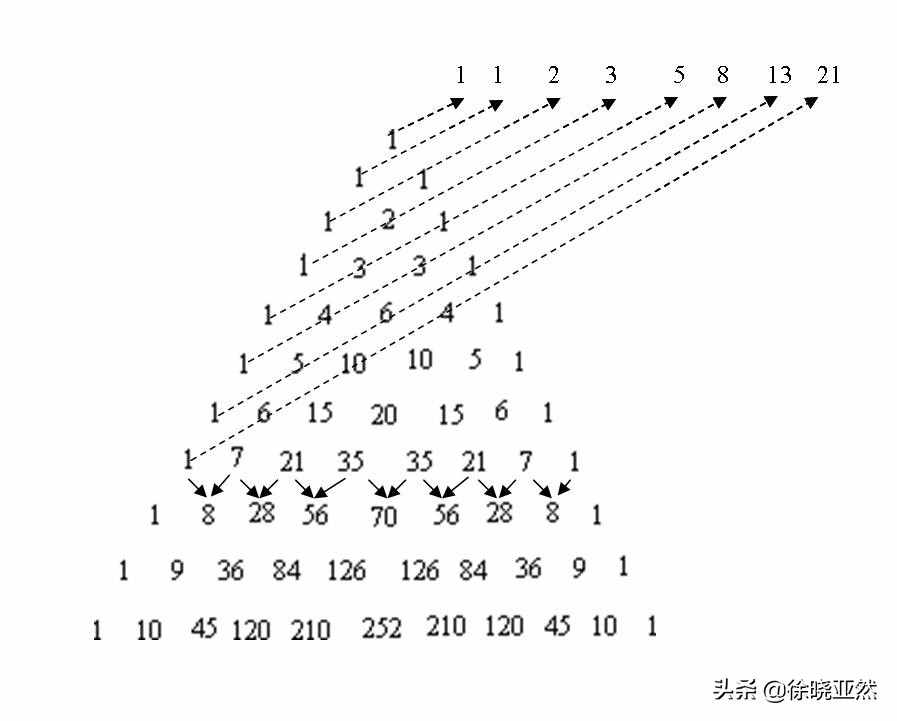
你可以很容易地从阳辉三角形中“找到”斐波那契数列

我们从杨辉三角形的初始1开始，以一定的角度画出一组平行线。这些平行线会在三角形中画出一系列元素，我们将这些三角形元素相加。如果平行线的角度正确，我们将得到斐波那契数列。事实上，这里隐藏着一个不太深的数学原理。利用斐波那契数列的通项公式和杨辉三角形的递推性质，我们可以用一种不太聪明的方法证明这个结论，这里不再赘述。

既然讲了数论，那怎么能不讲素数呢？于是就有了一个猜想：

斐波那契数列的元素中是否有无限多个素数？

如果你不小心，任何与素数有关的问题都会非常困难

其实不出所料，这个猜想至今还没有被证明。人们得出了一个弱化的结论，即在序数大于3之后，如果斐波那契数列的元素是素数，那么序数也一定是素数。值得注意的是，这个命题的对立面不成立！许多与素数有关的问题似乎都有类似的风格，轻描淡写，如此简单以至于无需任何数学知识即可理解。但是，很抱歉，通常要一百年左右才没有人解决它。斐波那契素数猜想也完全是这样的力量，哎，让人唏嘘不已！

斐波那契季度标志

上面提到的斐波那契数列的性质和应用，其实远不止这些。几乎每隔一段时间，数学界就会对这个序列做出新的发现。如果有一位著名而敬业的数学家只研究斐波那契数列，他一生都很难发现这个数列的所有性质，甚至他的高生产力也会让人惊叹不已。我们可以称这样的数学家为“斐波那契科学家”，就像我国研究红楼梦的专家一样，可以称其为红色科学家。正是因为斐波那契数列能够保证这样的结果的输出，1963年美国发行了《斐波那契季刊》( )，专门发表关于这个数列的研究成果，而且这个期刊仍然每年都出版。以发行速度发布，甚至成立了斐波那契数委员会。

在数学中，几乎不会再出现斐波那契数列有内涵的数学概念了。这样一个简单的数字序列跨越了许多数学领域，而在这些领域中，我们也看到其中涉及的问题深度不同。对于数学家来说，她就像一个既熟悉又陌生甚至害怕的朋友。你永远不知道她美丽的脸庞下隐藏着多少秘密。