冶金物理化学【10】 --- 相图基础
固溶体就是固态的溶液
相变化包括旧相消失,新相形成
根据独立组元数我们可以分为单元相图,二元相图和三元相图
f:自由度 ,K:体系的组元数
上面这个是体系中的相数,2表示影响组元数的温度和压力这两个物理量
凝聚体系忽略压力的影响,所以 2- 1,一个体系中相数最少为1,二元凝聚体系最多有两个两个独立变量,所以可用二维平面图来描述
对于三元凝聚体系则是最多有三个独立变量,所以可用三维空间立体图来描述
关于杠杆规则后面还有讲解
开始介绍二元相图
在上图中需要说明的是我们常用的二元凝聚体系,所以有K =2 ,然后后面那个2要减去1变为1
共晶反应:液相中同时析出两个固体
横坐标越靠近A表示A的含量越大,越靠近B表示B的含量越大
在左半边的弧线上降温,降温到弧线上时,液相中开始析出A,A的含量降低,此时点沿着弧线往A含量降低的方向移动,直到移动到共晶点 --- 开始发生共晶反应
此时过共晶点的横线被称为零变量线,简称零点线(此时液相L,固相A,B三相共存,自由度F=0)
如果温度再降低 --- 则只有A B两个固相存在了
左边那个交点被我们称为包晶点,过这个点横线是包晶线,在包晶线上发生的反应是液相L和固相A共同反应生成AmBn
这一部分再降温其实就是A和B反应生成AmBn
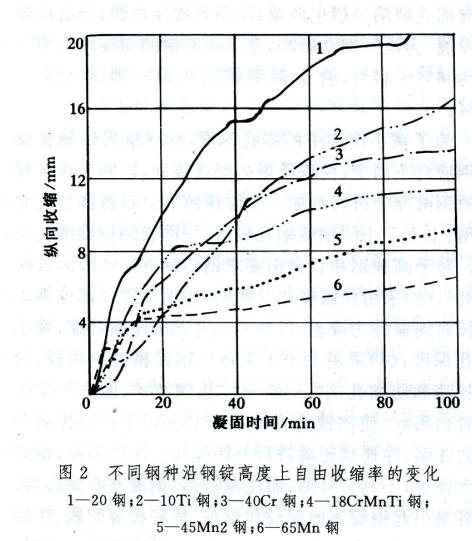
中间那条横线对应的是固相A,B的晶型转变温度,横线上方和横线下方的区别就是上方A,B的
晶型与下面的晶型不同
首先这不是一个包晶反应
判断方法:如果过交点的横线两头没有靠着两条竖线的话他就不是共晶反应
那这是个啥呢?答案是液相分层
注意这里只有右边那个半圆是液相分层,从这个半圆的圆顶开始降温液相L会分为液相L1和液相L2
L1的组成是A多B少,L2的组成是B多A少(相对于L的组成)
此时中间那个点是偏晶点,过该点的横线为偏晶线,发生的反应是偏晶反应 --- L1分解为固相A和液相L2
注意这个共晶反应依然是液相L分解为固相A和B
共晶反应的反应物是共晶点正上方的物质,生成物是过共晶点的横线左右两边相交的物质
连续固溶体型只有在A,B之间能够无限混溶的时候才能够出现
然后这个相图中液固两相中的组成该如何看呢 ---
首先靠近液相的是液相线,靠近固相的是固相线
然后以降温为例:
不停的降温,降到液相线之后有一个交点,过交点做横线,此时与液相线的交点是液相点,与固相线的交点是固相点
过点再作竖线,与X轴的交点就分别表示液相和固相中的A,B组成了
然后随着温度的降低液相点沿着液相线变化,固相点随着固相线变化
问固液两相各占体系的百分比怎么算呢? --- 答案是连接对应温度下的固相点和液相点,然后用杠杆定理求出固相和液相的百分比
上面的是有最高熔点,下面的是有最低熔点,分析方式和左边那个一致
左边相图分析:
注意这个相图中有两个固相As和Bs(因为没有无限互溶,都只有有限互溶)
左边顶上开始分析:首先液相降温,降温到液相线后开始产生固相,与此同时随着温度的降低,液相点随着液相线移动,固相点随着固相线移动
当到达中间这个交点时,液相同时析出固相As和Bs
过了同时析出的那条横线之后就只有固相了,此时固相As和Bs的组成由剩下的固相线来表示,这个剩下的固相线分别是靠近As的下半部分线和靠近Bs的下半部分那条线
下半部分那条横线是包晶线,这条包晶线上发生了一个新的包晶反应:
是液相L加上固相β生成固相α
α相的左右那两块之所以会出现是由于包晶反应中L和β过剩了
这里左边是L的液相线,下边那条是α的固相线
这里左边是阿尔法的固相线,右边是β的固相线
共析反应:从一个固相中析出另外两个固相
共晶反应:从一个液相中析出另外两个固相
包析反应:固相A加固相B生成固相C
包晶反应:液相A加固相B生成固相C
这一部分右边是α的固相线,左变这是阿尔法中有固相析出,左边是nanda的固相线右边也是阿尔法的固相线
温度不断降低到达中间那个交点(共析点)之后,固相α中同时析出nanda和β,发生共析反应
上面这个中间的交点是共晶点 --- 因为有典型的一液两固
注意这里的下半部分都是固相了
这里中间这个点是包析点 --- 因为是固相β和α反应生成了新固相nanda
相图总结
如果相图中有化合物生成的话,表示化合物那一条竖线与液相线交点处的斜率越大,生成的化合物越稳定,反之斜率越小,生成的化合物越不稳定
相图的基本原则 --- 单元,二元和三元相图均适用
如果相数相差不为1的话,则这两个相区只能以点接触的方式毗邻
上面这个图中的红色部分是液相单相
第一个相律的考点主要是:自由度 f = 0 的时候我们找到三相点,该点上的自由度f等于0,于此同时过该点的横线上的自由度也为0,所以该横线平行于x轴
上面第二图错在了出现四相共存的情况,横线上出现了四个点,在二元凝聚系中是不可能出现这种情况的
第三个图不符合相图原则二,单相区的两边界线之间的夹角应该小于180°