(《机器学习》完整版系列)第12章 计算学习理论——12
本章是机器学习的理论指导,并不涉及具体的算法,而是为算法提供理论依据。 本章涉及的概念较多,考虑到大多数读者不是从事理论研究,故我们在这里把一些概念具象化以帮助大家理解(当然会牺牲一些严谨性)。 而对于从事理论研究的同学,可以此理解作为基础,再进行修正、补充严谨性即可。
把二分类问题视为概念学习问题,让概念类 C \{C} C独立于具体的样例集 D D D而存在,讨论假设空间 H \{H} H与概念类 C \{C} C的关系。
1、假设 h h h与概念 c c c的适配:相等、近似相等以及几乎近似相等。
2、假设空间 H \{H} H对概念 c c c的覆盖情况:覆盖、近似覆盖以及几乎近似覆盖。
3、假设空间 H \{H} H对概念类 C \{C} C的覆盖情况:覆盖、近似覆盖以及几乎近似覆盖。
概念类与假设空间的关系
样本个体 x \{x} x组成的集合为 X \{X} X(这里可设 X \{X} X中的样本不重复,样本个体 x \{x} x呈现的“重复度”以概率分布 D \{D} D来描述),即以 ( X , D ) (\{X},\{D}) (X,D)描述样本空间,则在 ( X , D ) (\{X},\{D}) (X,D)中采样得到样本集: D = { x i } i = 1 m D=\{\{x}_i\}_{i=1}^m D={xi}i=1m,其中,可能有大量的重复样本,但编号(下标)不同。 若剔除重复样本,则要加上概率分布(或频度分布),即 D = ( D ′ , D ) D=(D',\{D}) D=(D′,D),其中, D ′ D' D′为没有重复样本的样本集。 对样本集 D D D中的样本配上它的标记,形成样例集,为方便仍用 D D D表示样例集,即由上下文确定 D D D表示样本集还是样例集。
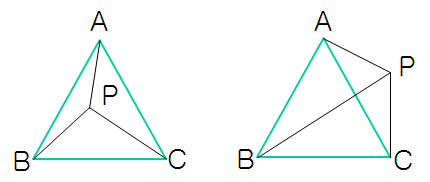
概念的“是”与“否”产生一个二分类问题(本章无特殊说明时,均指二分类),其中,肯定的回答产生样本空间 X \{X} X的一个子集,可视为其概念的外延,如,“三角形中是否有一个角为直角”,回答“是”的三角形组成一个集合(它为三角形集合的子集),这样就形成了“直角三角形”的概念:
内涵:有一个角为直角的三角形为直角三角形(定义方式通常是:最邻近的“种”加“属差”,如,直角三角形 = = =“三角形” + + +“有一个角为直角”)。
外延:所有的直角三角形。
综上,具有某共同特征的一个子集,一方面反映一个概念,另一方面就是某二分类问题的一个分类,综合二者:即概念 c c c表示 X \{X} X到 Y \{Y} Y的映射( y = c ( x ) y=c(\{x}) y=c(x)),其中, Y \{Y} Y为二值,如 y ∈ { − 1 , 1 } y \in \{-1,1\} y∈{−1,1}(如无特殊说明,本章取二分类的标记为 { − 1 , + 1 } \{-1,+1\} {−1,+1},其中,正例的标记为 + 1 +1 +1)或 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1},显然,由概念产生的二分类中没有矛盾样例。
X \{X} X到 Y \{Y} Y的任一映射,都可以定义一个概念 c c c,体现 y = c ( x ) y=c(\{x}) y=c(x)。 这样,基于 X \{X} X就可以定义无穷多概念(当 X \{X} X有无穷多个样本时),如, X \{X} X为“全体三角形”,在其上进行二分类: 直角三角形 ∪ 非直角三角形 \text{直角三角形}\cup \text{非直角三角形} 直角三角形∪非直角三角形、 至少有一个角为45度的三角形 ∪ 没有角为45度的三角形 \text{至少有一个角为45度的三角形}\cup \text{没有角为45度的三角形} 至少有一个角为45度的三角形∪没有角为45度的三角形、 等腰三角形 ∪ 非等腰三角形 \text{等腰三角形}\cup \text{非等腰三角形} 等腰三角形∪非等腰三角形、 ⋯ ⋯ \cdots \cdots ⋯⋯,每一个分类的正例集即是一个概念。 在这些概念中,有的概念人们取了名字(如,直角三角形),有的没有取名字(如,非等腰但有直角的三角形)。
现在把二分类问题视为概念学习问题,即原来的任务:“你参考这个样例集 D D D,把 X \{X} X进行二分类”,变为任务:“你参考这个样例集 D D D
,在 X \{X} X上定义一个反映正例的概念 c c c”。
从“符合(或近似符合、尽可能地符合)给定的样例集 D D D”这一要求出发,可能得到不只一个概念,例如,样例集 D D D的正例为“等腰直角三角形”,反例集中没有“等腰三角形”也没有“直角三角形”,你可能只观察到样例集 D D D中全是“直角三角形”,因此你定义样例集 D D D为概念: c 1 = c_1= c1=“直角三角形”;他可能只观察到样例集 D D D中全是“等腰三角形”,因此他定义样例集 D D D为概念: c 2 = c_2= c2=“等腰三角形”;还有人可能观察到样例集 D D D中全是“直角三角形且等腰三角形”,因此他可定义样例集 D D D为概念: c 3 = c_3= c3=“等腰直角三角形”,那么, 这些概念就都是目标概念(想起“盲人摸象”的故事没有?),目标概念的全体形成一个集合,称为概念类,记为 C \{C} C,目标概念 c ∈ C c\in \{C} c∈C形成 X \{X} X到 Y \{Y} Y的映射,且在样例集中有 c ( x ) = y c(\{x})=y c(x)=y,如图12.1 所示。
图12.1 目标概念
当然,你不知道 C \{C} C中具体是些什么(否则不用学习了),你把这个新的任务交给算法 L \{L} L,它学习的目的就是寻找目标概念, L \{L} L在样例集 D D D的约束(或称监督)下,找到了自认为的“目标概念”(人们称其为假设) h h h,当然,从算法 L \{L} L的能力上讲,它可以找到很多假设 h h h,这是由于设置算法不同的“超参”、不同的初始化、不同的终止条件等。 假定算法 L \{L} L尽其所能找出所有的基于样例集 D D D的假设,形成假设空间 H D \{H}_D HD。 现在有两个集:真正的目标概念组成的概念类 C \{C} C和算法 L \{L} L自认为的“目标概念”形成的假设空间 H D \{H}_D HD。
若 c ∈ H D c\in \{H}_D c∈HD,则 H D \{H}_D HD中存在假设(至少有 c c c)在样例集 D D D上产生一致性的二分类,称该问题对学习算法 L \{L} L是“可分的”,亦称“一致的”,如图12.2 ( c ∈ H D c\in \{H}_D c∈HD)所示。
图12.2
下面设 c ∉ H D c \notin \{H}_D c∈/HD,如图12.3 ( c ∉ H D c\notin \{H}_D c∈/HD)所示。
图12.3
但图12.3隔得太开了,我们依靠想像研究具有某种“接近”的情况,例如,设想一下:当 H \{H} H为一个开区域,而 c c c为边界上的一点,则 c c c虽然不属于 H \{H} H,但离 H \{H} H中的点要多近有多近。
从概率角度,现实中的样本空间 X \{X} X,常常带有一个真实的分布 D \{D} D,例如,现实中“学生画的三角形”,包含两个方面:一是不同三个角形各一个样本形成的样本空间 X \{X} X,二是基于学生的喜好选择,形成的分布 D \{D} D,如,像“针尖细的角”的三角形就非常罕见,对它属于什么三角形的判断是否正确就可以忽略。 也就是说在进行度量时要考虑分布 D \{D} D。
基于概率角度(考虑分布 D \{D} D),【西瓜书式(12.1)(12.2)】定义了二分类上的假设 h h h的泛化误差和经验误差,有两种误差度量:一是泛化误差【西瓜书式(12.1)】,它是随机采样“一个样本”的度量(的数学期望),是概率意义下的;二是经验误差【西瓜书式(12.2)】,它是对数据集 D D D上“所有样本”的误差求平均值,即转化为“一个样本”的度量(均值)。
定义误差函数
e ( h , x ) = { 0 , 若 h ( x ) = c ( x ) 1 , 若 h ( x ) ≠ c ( x ) \begin{align*} e(h,\{x}) = \begin{cases} 0,\quad \text{\text{若}$h(\{x})= c(\{x}$}) \\ 1,\quad \text{\text{若}$h(\{x})\neq c(\{x}$}) \\ \end{cases} %\tacg{eq:c12-01a1} \end{align*} e(h,x)={0,若h(x)=c(x)1,若h(x)=c(x)
E ( h ) = E x ∼ D ( e ( h , x ) ) = P x ∼ D ( h ( x ) ≠ c ( x ) ) × 1 + P x ∼ D ( h ( x ) = c ( x ) ) × 0 = P x ∼ D ( h ( x ) ≠ c ( x ) ) \begin{align*} E(h)= & \{\{E}}\{\{x}\sim \{D} } (e(h,\{x}))\notag \\ = & P_{\{x}\sim \{D} }(h(\{x})\neq c(\{x}))\times 1+ P_{\{x}\sim \{D} }(h(\{x})= c(\{x}))\times 0\notag \\ = & P_{\{x}\sim \{D} }(h(\{x})\neq c(\{x})) %\tcag{eq:c12-01a2} \end{align*} E(h)===x∼DE(e(h,x))Px∼D(h(x)=c(x))×1+Px∼D(h(x)=c(x))×0Px∼D(h(x)=c(x))
从式子的右边可知, E ( h ) E(h) E(h)与分布 D \{D} D相关,若是要强调这一点,则记为 E ( h ; D ) E(h;\{D}) E(h;D)。
如果二分类是基于概念 c c c的,则有对应的泛化误差和经验误差,如,由概念 c c c导出二分类 h h h,其泛化误差为
E ( h ) = P x ∼ D ( h ( x ) ≠ c ( x ) ) \begin{align} E(h)=P_{\{x}\sim \{D} }(h(\{x})\neq c(\{x})) \tag{12.1} \end{align} E(h)=Px∼D(h(x)=c(x))(12.1)
将 h h h的经验误差【西瓜书式(12.2)】视为 h h h与 c c c在数据集 D D D上的“距离”,故对应地,直观上将 h h h的泛化误差视为 h h h与 c c c在 X \{X} X上的“距离”, E ( h ) ⩽ ϵ E(h)\ \ E(h)⩽ϵ直观上如图12.4 (限定 h h h与 c c c的“距离”范围])所示。
图12.4
现在我们将前述的样例集 D D D改为 ( D ∼ D , ∣ D ∣ = m ) (D\sim \{D},|D|=m) (D∼D,∣D∣=m),即让 D D D在约束下变化(采样生成),在此条件下算法 L \{L} L形成更大的假设空间
H m = ⋃ D ∼ D ∣ D ∣ = m H D \{H}_m =\{\}\{\{D\sim \{D}\\|D|=m}} \{H}_D Hm=D∼D∣D∣=m⋃HD
若再取消样本数 m m m的限制,则算法 L \{L} L形成更大的假设空间
H = ⋃ m H m \{H} =\{\}\ \{H}_m H=m⋃Hm
H \{H} H与 C \{C} C的关系能充分体现算法 L \{L} L的能力。
对于样本空间 X \{X} X而言,学习算法 L \{L} L一定有一个假设空间 H \{H} H,但反过来,一个假设空间 H \{H} H有许多学习算法 L \{L} L,学习算法 L \{L} L与假设空间 H \{H} H的关系就像函数与其值域的关系。
现在让假设空间 H \{H} H独立于具体算法 L \{L} L而存在,同样地,让概念类 C \{C} C独立于具体的样例集 D D D而存在,讨论假设空间 H \{H} H与概念类 C \{C} C的关系。
I. h h h与 c c c
度量假设空间 H \{H} H中的假设 h h h与概念 c c c的适配情况(逐步放松):
(1)若 E ( h ) = 0 E(h)=0 E(h)=0,则表示 P ( h = c ) = 1 − P ( h ≠ c ) = 1 P(h=c)=1-P(h\neq c)=1 P(h=c)=1−P(h=c)=1。 视为 h = c h=c h=c。
(2)若 E ( h ) ⩽ ϵ E(h)\ \ E(h)⩽ϵ,则视为 h ≈ c h\ c h≈c,其近似程度用“ ⩽ ϵ \ \ ⩽ϵ”来刻画,如图12.4 所示。
(3)若
P ( E ( h ) ⩽ ϵ ) ⩾ 1 − δ \begin{align} P(E(h)\ \ )\ 1-\delta \tag{12.2} \end{align} P(E(h)⩽ϵ)⩾1−δ(12.2)
则视为“几乎” h ≈ c h\ c h≈c,其近似程度用“ ⩽ ϵ \ \ ⩽ϵ”来刻画,“几乎”程度由“ ⩾ 1 − δ \ 1-\delta ⩾1−δ”来表达。 换言之,其程度体现在两个参数上:精度要求( ϵ \ ϵ靠近0)和置信度要求( 1 − δ 1-\delta 1−δ靠近1)。 直观上这样理解:由于 E ( h ) E(h) E(h)与分布 D \{D} D相关(即 E ( h ; D ) E(h;\{D}) E(h;D)),让 D \{D} D变化,则 h h h实际形成曲线 h ( D ) h(\{D}) h(D),对应于图12.4 实际为一根以为 h ( D ) h(\{D}) h(D)心、以“ ϵ \ ϵ为半径的曲折“管子”(图12.4 为其截面),(2)的情况是: c c c一直在“管子”内,(3)的情况是: c c c在“管子”内的长度占比很大(“ ⩾ 1 − δ \ 1-\delta ⩾1−δ”)。
显然,(2)成立时,(3)一定成立,所以,我们重点关注(3)。
h h h是否满足(2)和(3)与给定的参数 0 < ϵ , δ < 1 0